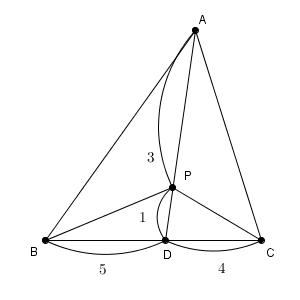
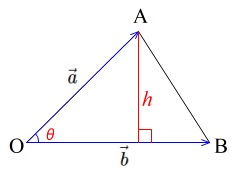
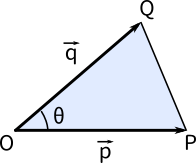
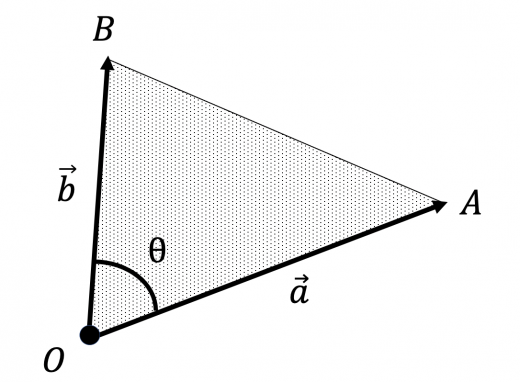
まず、三角形 に対し、 OA → = a →, OB → = b → とし、 ∠ AOB = θ とします。 すると、この三角形の面積 は、上で見た内容を使えば S = 1 2 a → b → sin θ となります。 内積で
ベクトル 面積 公式 外積-ラプラシアン (ベクトル場) ∇ 2 A r = ∇ 2 A r − 2 r 2 ∂ A θ ∂ θ − 2 r 2 sin θ ∂ A ϕ ∂ ϕ − 2 A r r 2 − 2 cot θ A θ r 2 {\displaystyle \mathbf {\nabla } ^{2}\mathbf {A} _{r}=\mathbf {\nabla } ^{2}A_{r} ベクトルでいうところの掛け算ですが、ベクトルの問題ではよく求めさせられますよね。 この内積が入った三角形の面積を求める公式があります。 それがこれです。 図のような三
ベクトル 面積 公式 外積のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
 | ||
「ベクトル 面積 公式 外積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「ベクトル 面積 公式 外積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | 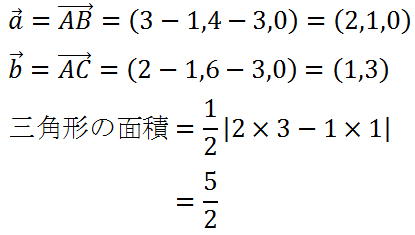 | |
 |  |  |
「ベクトル 面積 公式 外積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  |  |
「ベクトル 面積 公式 外積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
 |  |  |
「ベクトル 面積 公式 外積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
 |  |  |
「ベクトル 面積 公式 外積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 | ||
「ベクトル 面積 公式 外積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「ベクトル 面積 公式 外積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |
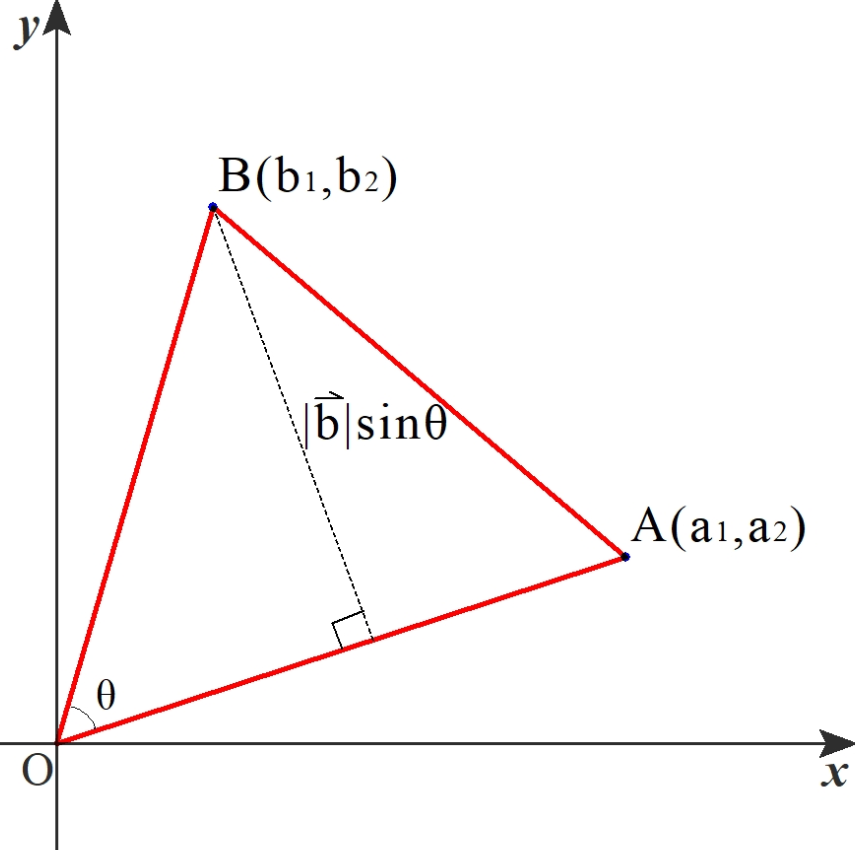
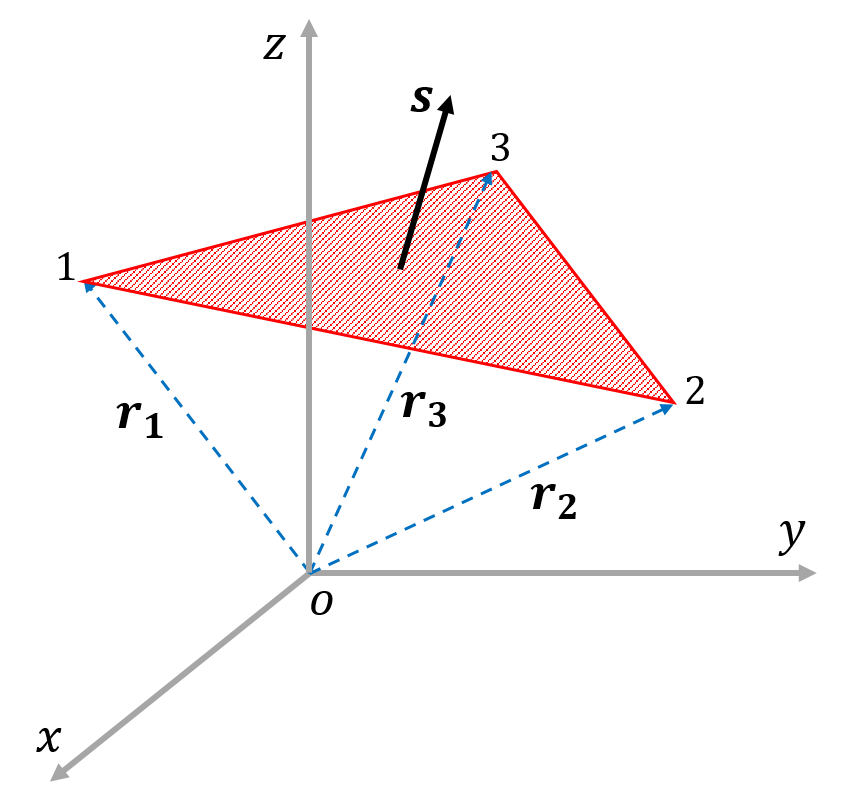
こうして計算した量を、 ベクトル関数 \overrightarrow {F} F の面積分 といいます。 ベクトル関数を面積分するというのは、ベクトルそのものを何か足し合わせていくような操作をするわけではな平行四辺形の面積は (底辺 w w) \times × (高さ h h) で求められます。 ベクトル \overrightarrow {a} a と \overrightarrow {b} b を平行でない二辺とする平行四辺形を考えます。 それらのなす角は
Incoming Term: ベクトル 面積 公式, ベクトル 面積 公式 証明, ベクトル 面積 公式 覚え方, ベクトル 面積 公式 空間, ベクトル 面積 公式 平行四辺形, ベクトル 面積 公式 サイン, ベクトル 面積 公式 なぜ, ベクトル 面積 公式 外積, ベクトル 内積 面積 公式,




0 件のコメント:
コメントを投稿