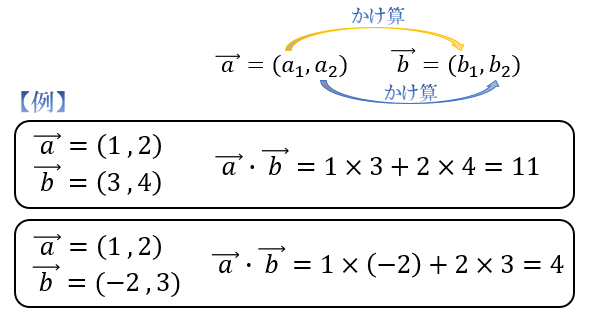
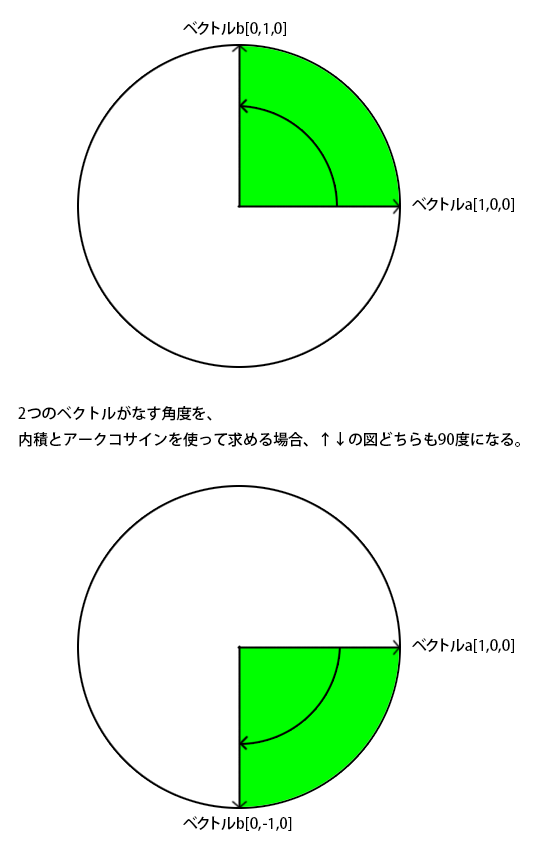
平面の法線ベクトル a&b& の長さは、平行四辺形の面積 u S に等しい b & a & S ab && u a,b & が作る平行四辺形を含む面に 垂直で、長さが1のベクトルを法線ベク トルといい、 a b a b S a bベクトルのなす角は内積の公式を使って求めます。ベクトルの内積は、それぞれのノルムとなす角のコサインの積です。 arccos 関数でコサインから角度(ラジアン)を求めるつまり、ベクトルの内積とは、1行 n n 列の射影行列とベクトルの積であり、2次元や3次元のものを1次元化すること(=直線上に射影すること)なのです。 以上がベクトルの内積の意味です。 余談ですが、このようにベクトルを行列のように扱ったり、反対

数bの問題です 空間ベクトルの範囲です なぜ下線部のようになるかわかりません Clear
ベクトル 角度 公式
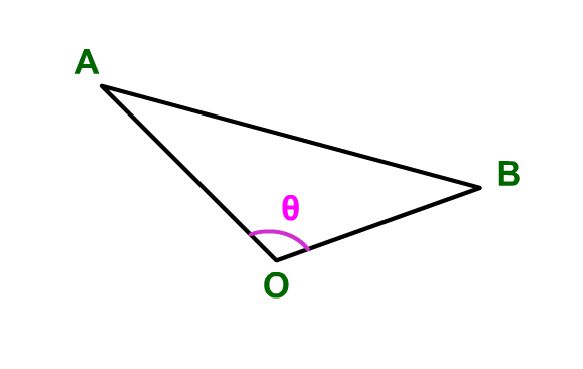
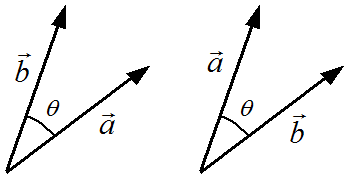
ベクトル 角度 公式-32 A B cosθ (35) スカラー積は記号 A ・B (36) で表す。 スカラー積は角度θにより− A B から A B までの値をとる。 物理学で用いられるスカラ ー積の例は力Fが質点の変位sで行う仕事 ・F sなどである。 •A B = A B cosθ スカラー積 ベクトル積ベクトルの内積 解説 ベクトルのなす角 2つのベクトル の始点を原点Oに重ねて, とするとき,∠AOB=θをベクトルの のなす角という。 ただし,0°≦θ≦180°とする。 ベクトルの内積の定義 2つのベクトル のなす角をθとするとき,ベクトル の内積 を次



Studydoctor立方体と空間ベクトルの内積 数b Studydoctor
ベクトルの足し算(図の場合、成分の場合) 方向ベクトルの意味と2通りの求め方 内積の意味と3つの公式 ベクトルのなす角度の計算(2次元、3次元)と検算ツール 等差数列の一般項の求め方の証明と例題角度計算ツール a → = ( a 1, a 2, a 3) と b → = ( b 1, b 2, b 3) のなす角 θ を計算してくれるツールです。 平面ベクトルの場合は、 a 3 = b 3 = 0 としてください。 ※あくまで計算の確認程度にお使いください。 次回は 等差数列の一般項の求め方の証明と例題 を算の一つである。なぜならば、内積は二つのベクトルの角度を示す指標になるものだからである。 まず、内積の定義を示す。 ベクトルの内積の定義 ベクトルP、Q の内積はP¢Q と表記し、以下のような公式で与えられる。 P¢Q = i=1 PiQi
三角関数は周期関数なので、逆関数は多価関数である。 逆関数の性質から以下が成り立つ: =,() = / /ピタゴラスの定理 ピタゴラスの定理やオイラーの公式などから以下の基本的な関係が導ける 。 = ここで sin 2 θ は (sin(θ)) 2 を意味する。 この式を変形して、以下の式が導かれる:例15 ベクトル −→ ab = (−2, 1, 2) とベクトル −→ ac = (1, −1, 0) を2 辺とす る三角形abc について,頂角a の角度(∠bac)と,中線am の 長さを求めよ. (岐阜大) 解cos∠bac = −→ ab−→ ac ab·ac = −211(−1)2·0 (−2)2 12 22 12 (−1)2 02 = − 1 √ 2Cが右手系3 を作る向きとする.このように方向を定めると, A B = B A
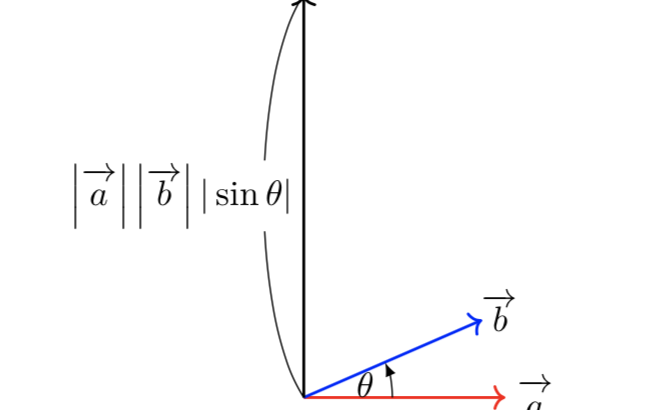
複素数 z = x yi の偏角は、 arg z と書かれ、正の実 軸から動径 Oz までの角度を反時計回りに測った角度である。 弧度法で表示する。時計回りに測ると負になる。 複素数に対する偏角の表示を一意にするために、主値を区間 (−π, π に制限する。 0, 2π) にすることもある。ベクトルと力方向の角度θによって変化。 力が斜めに作用する場合の力のモーメント θ r F 軸 F r 並進 θ モーメントアーム(moment arm):r →回転軸と力の作用線を結んだ垂線 大きさと方向を持つベクトル量 方向→反時計回り(+)・時計回り(-)と書く.演算の結果のCはベクトルである.その大きさは, jCj = jAjjBjjsin j (11) とする.ここで, はそれぞれのベクトルの間の角度である.一方,その方向はAとBの 定める平面に垂直で,A;




高校数学b 平面ベクトル 公式一覧 内分 外分 面積 学校よりわかりやすいサイト




平面ベクトルの定義と公式 足し算 絶対値 内積 なす角の求め方 Irohabook
基本ベクトルの関係を導き出してみます。 XY座標系の基本ベクトルをx, yとします。 UV座標系の基本ベクトルをu, vとします。 XY座標系とUV座標系の原点は同一とします。 xからuへ回転する角度をθとします。 このときu, vはx, yを用いて、下記の様に表せます。 21年2月19日 この記事では、「ベクトルを使った三角形の面積の求め方」について、できるだけわかりやすく解説していきます。 公式の証明や計算問題なども解説していきますので、この記事を通してぜひマスターしてくださいね。 目次 非表示 角度は、次の2段階のステップで求めます。 求める角度の余弦(cos(コサイン))を求める。 余弦から角度を求める。 第1ステップで余弦定理を使います。 余弦定理の公式を覚えていればそれに当てはめるだけで余弦が求まります。 辺から余弦(コサイン)を求める



1




ゲーム数学 2つのベクトルのなす角度 ねこじゃらシティ
ベクトル図から判断できるように、実数軸上の P=EIcos(θ 1 −θ 2) は有効電力(消費電力)となり、虚数軸上の Q=EIsin(θ 1 −θ 2) は無効電力、ベクトル の絶対値は皮相電力を表している。 は皮相電力の複素数表示であることが分かる。皮相電力を K として、要点をまとめておくと次のようになる。25 ベクトルの外積 ベクトルの外積は、次のように定義される。ベクトルa とb について、それらがなす 角度を (< ˇ) とするときベクトルの外積a b は、大きさが ja bj = jajjbjsin (1) で、ベクトルa とb の両方に垂直、方向がa、b、a b の順に右手系をなすようなベク トルである。 また、 基本ベクトルの内積 で見た通り、内積は、ベクトルの大きさとなす角を使って表すこともできます。 なす角を θ θ とおけば θ となります。 θ = 1 2 θ = 45 ∘ となります。 これが答えです。 ちなみに、この問題は、図形的に解くこともでき



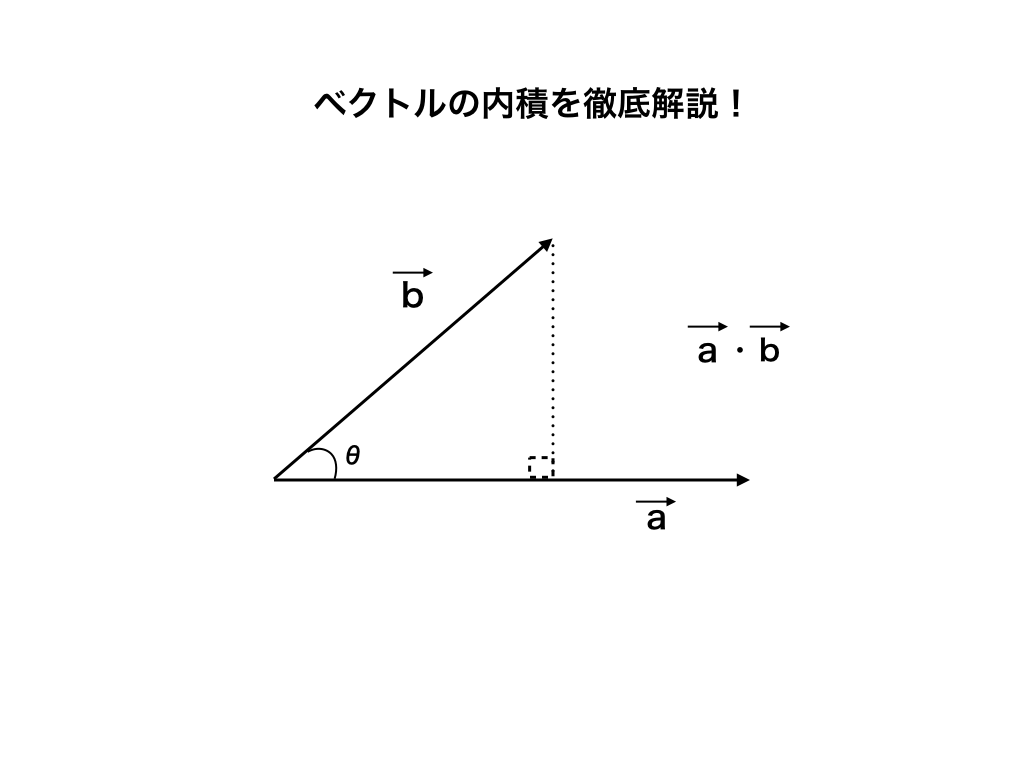
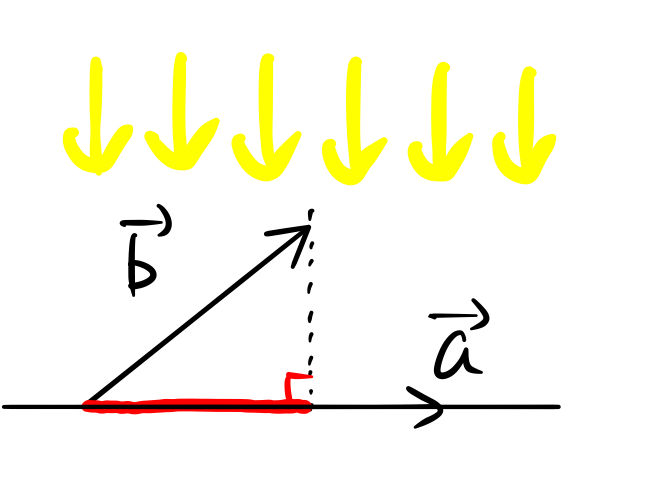
内積とベクトルの長さ



48s96ub7b0z5f Net Kuukan Bekutoru Naiseki
1 ベクトルの基礎 6/14 B A A B B A u A B A Bsin 図16 ベクトルの外積 平行四辺形の面積 は図16に示す2つのベクトルのなす角度である.方向を表すuは単位ベクトルで,ベク トルAを Bの方に向かって回したときに,右ネジの進む方向と定義する.ベクトルの大き さは,右図のようにベクトルAと Bが作ベクトルaと bの角度関係 ⇒ a b aとbの角度関係 cos ab a ・b=0で =90°となることから、 内積を見ることでベクトル同士の直交関係を把握しやすい。 内積の公式 (a b) c a c b c ( a) b a b 13/3/2 「数値流体力学」輪講 準備編 第2回 13ベクトルの大きさを求めることと、線分の長さを求めることは同じことといっても良いですが、 ベクトルの内積を利用する際の求め方でやってはいけない注意点とともに基本的な問題で復習しておきましょう。 ベクトルな便利さ 三角比の余




ベクトル角公式 Invale2 2




Houdiniメモ Vex 二つのベクトルがなす角の計算 Rn Works
数学公式 ベクトルの大きさ(長さ) $$ \mid \vec{a} \mid = \sqrt{a_1^2 a_2^2} $$ 内積の定義 $$ \vec{a} \cdot \vec{b} = \mid \vec{a} \mid \mid「単位ベクトル を軸とし、角度 だけ右ねじ回転するような変換」を表す回転行列 は、以下のロドリゲスの回転公式で与えられる: ただし、 は以下の102注2で定義されるベクトルのクロスである。5.ベクトル積について 2つのベクトル , によってつくられる平行四辺形の面積を,この面に直角の方向をもったベクトル , のベクトル積といい, で表す。 ベクトル積のことを外積(outer product)という。べクトル積の大きさは,2つのベクトルのなす角がθ




ベクトルの公式一覧 計算 内積 三角形の面積 共線条件 理系ラボ




2つのベクトルのなす角8を求めよ 途中の計算のやり方が分かりません どうやったら Clear
こんにちは、ウチダです。 今日は数学bで習う 「ベクトル」 について、まずは足し算引き算(分解・合成)や成分表示などの基本的な事項を見ていきたいと思います。 また、ベクトルの意味や使い方も、物理学や数学、日常会話といった、いろんな立場からの見解を簡単に見ていきま空間のベクトルでは、平面の時と比べてパラメータが1つ増えますが、平面上のベクトルの公式等がそのまま使えます。 空間のベクトルでの公式 空間のベクトルでも同じように成立する公式を紹介していきます。まず、2点\(A(x_1 , y_1 , z_1) , B(x_2 , y_2 , z_2)\) 間しかしこの問題では,角度そのものではなく角度差の符号を求めればよいので, 逆三角関数を使う方法よりも簡単で優れた,外積を使う方法を紹介します. 2つの2次元ベクトル A=(Ax, Ay), B=(Bx, By) の外積を次のように定義する. A × B ≡ Ax * By - Ay * Bx



3点の座標から簡単に角度と回転方向を求める 2 3 N次元 外積を用いる方法



内積とは何なのか ベクトルの内積の2つの求め方とその活用法 アタリマエ
算数数学個別指導の中山先習塾の映像授業です。 高2「ベクトル、角度、余弦定理、内積」 中山先習塾の公式サイト( httpsそもそも,ベクトルの成分と角θをつなぐ公式 (1)は ではなく の形をしており, cos θ の値までしか求まらない. このような問題では,必要に応じて「 θ は となる角」などと文章で答えます. 例題1 のとき2つのベクトル のなす角θを求めなさい四元数と三次元空間における回転 レベル 大学数学 座標,ベクトル 更新日時 ハミルトンの四元数(クォータニオン,quaternion) について基礎から解説します。 三次元空間における回転の記述を理解することが目標です。




ベクトルの公式一覧 計算 内積 三角形の面積 共線条件 理系ラボ




平面ベクトルの定義と公式 足し算 絶対値 内積 なす角の求め方 Irohabook
2つのベクトルのなす角 ベクトル を平行移動し一方のベクトルの始点を他方のベクトルの始点に重ねた場合に2つのベクトルで作られる角度の180°以下となる方の角度を2つの ベクトルのなす角 という.(下図を参照のこと)2つのベクトルのなす角 ベクトル を平行移動し一方のベクトルの始点を他方のベクトルの始点に重ねた場合に2つのベクトルで作られる角度の180°以下となる方の角度を2つの ベクトルのなす角 という.(下図を参照のこと)上では図からただちに、方向余弦の式を求めました。 ここでは内積の計算をすることで、同じ式が求められるか確かめてみましょう。 ベクトル v → \overrightarrow {v} v は基本ベクトルを使って次のように書けます。 v → = v 1 i → v 2 j → v 3 k




ベクトル編 内積と外積を画像付きで徹底解説 大学1年生もバッチリ分かる線形代数入門




二直線のなす角を求める2通りの方法と比較 高校数学の美しい物語
ベクトル方程式の公式一覧 ベクトル方程式の公式をまとめました。全て丸暗記する必要はありませんが, のベクトル方程式は?と聞かれたときにすぐに立式できるようになっておきましょう。 → ベクトル方程式の公式一覧ベクトルの平均 角度Θ、長さRのベクトル x成分y成分 x成分 y成分 ①平均値はで表す x j≡ 1 N x j j ∑ ②複素平面だとおもうと便利 ReiΘ= 1 N eiθ j j ∑=eθ j eiθ=cosθisinθ実数部がx成分、虚数部がy成分 オイラーの公式 Re Im 同じ 記法の注①② ベクトルの有限回転 ベクトル を, と並行ではない単位ベクトル の回りに,角度 だけ回転させたものを とします.回転の方向はネジを回すとベクトル の方向にネジが進むような方向です.つまりは,次の図のような状況を考えているわけです.目標は, を , , で表すことです.頑張り



ベクトルのなす角度 Thoth Children



ベクトルの内積
(B)ベクトルの回転 一方、ベクトルmの回転は座標の回転と逆なので、mをx 軸のまわりにγ 回転してMに する回転行列Rは R 100 0cos sin 0sin cos x γ γγ γ γ ⎛⎞ ⎜ =⎜− ⎜⎟ ⎝⎠ ⎟ ⎟ (A 16) で、 () MR= x γm (A 17) と書くことができる。 同様に、y 軸回りに定義1 角度で方向を指定する場合の方向微分の定義-ベクトルを使わない表現・「 n変数関数y=f (x 1,x 2,,x n)は、点(a 1, a 2, ,a n)において、 x 1 軸プラス方向に対して角度θ 1 方向 x 2 軸プラス方向に対して角度θ 2 方向 x n 軸プラス方向に対して角度θ n 方向



空間ベクトルとは 内積 面積などの公式や問題を解くコツ 受験辞典




高校数学b 空間ベクトルのなす角の計算 映像授業のtry It トライイット



Coyote流テクニカルtips Tips 03 Maya ベクトルの活用 内積 外積 三角関数 連載 Cgworld Jp




高校数学b 余弦定理のベクトル表示と内積の定義の成分表示の証明 受験の月




勉強しよう数学 ベクトルの回転移動と三角関数の加法定理




C プログラム上での数式と数学上での数学の違いについて知りたい また式の落とし込み方は合っているのか Teratail




ベクトルの内積の公式から 平行条件 垂直条件 成分との関係までわかりやすく解説 高校生向け受験応援メディア 受験のミカタ



ベクトルについて




基本 ベクトルの内積となす角 なかけんの数学ノート



ベクトルの内積となす角8の問題です 1 A 2 3 B 1 Yahoo 知恵袋



Studydoctor立方体と空間ベクトルの内積 数b Studydoctor



法線 法線ベクトルとは 方程式 2 直線のなす角の求め方 受験辞典



1



ベクトルの内積 スカラー積 と外積 ベクトル積 の成分表示



ベクトルの外積の公式やその覚え方とは 高校範囲で役立つ場面についても解説 東大医学部生の相談室
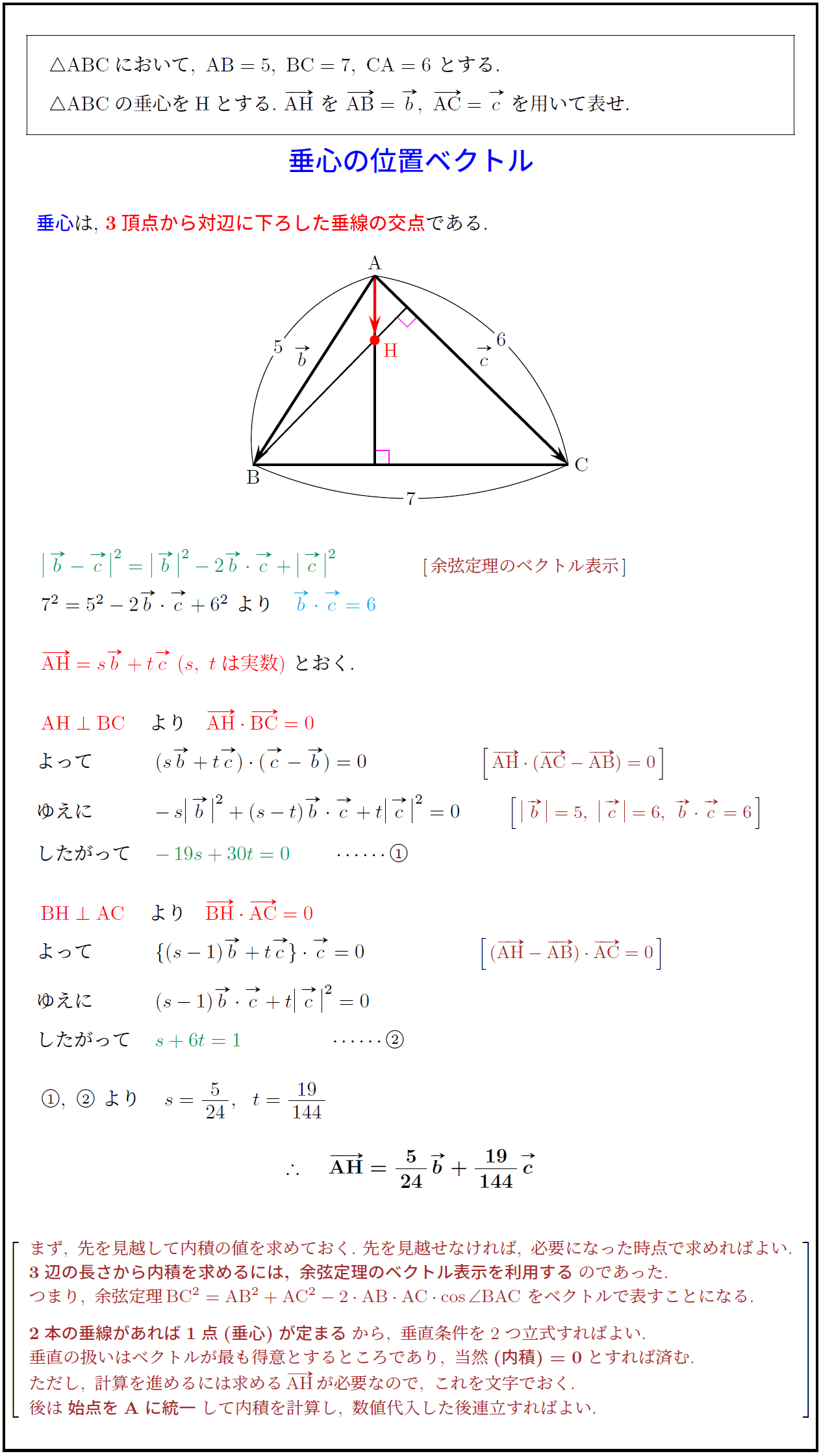



高校数学b 三角形の垂心の位置ベクトル 受験の月



ベクトルの内積 定義の意味と活用方法 ここからはじめる高校数学




高校数学b 角の二等分線のベクトル2パターン 受験の月




ベクトルの内積の全てを超わかりやすくまとめた 意味 公式 成分計算 理系ラボ



ベクトルの内積とは 意味 公式や求め方 計算問題 受験辞典




と で図の矢印の向きが違う意味がわかりません Clear




2つのベクトルのなす角8を求めよ 途中の計算のやり方が分かりません どうやったら Clear




高校数学b 空間ベクトルのなす角の計算 例題編 映像授業のtry It トライイット



ベクトルのなす角
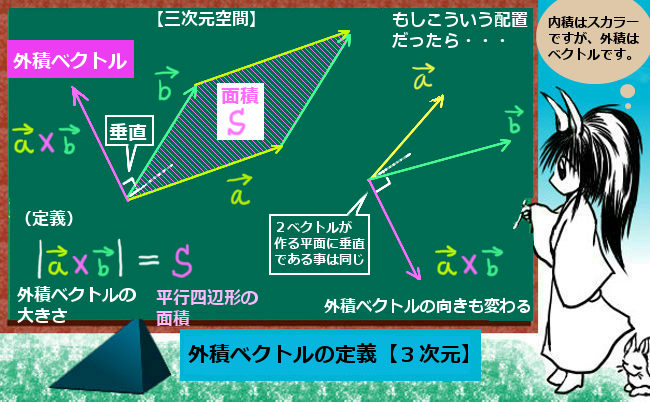



外積ベクトルの定義と公式 3次元 理数系無料オンライン学習 Kori



数学 内積ってなんぞ その2 角度とcg編 No More Retake



空間ベクトルとは 内積 面積などの公式や問題を解くコツ 受験辞典




内積とは何なのか ベクトルの内積の2つの求め方とその活用法 アタリマエ



ベクトルの内積 をシミュレーション 図解で理解しよう 数学入門




ベクトルの公式一覧 計算 内積 三角形の面積 共線条件 理系ラボ
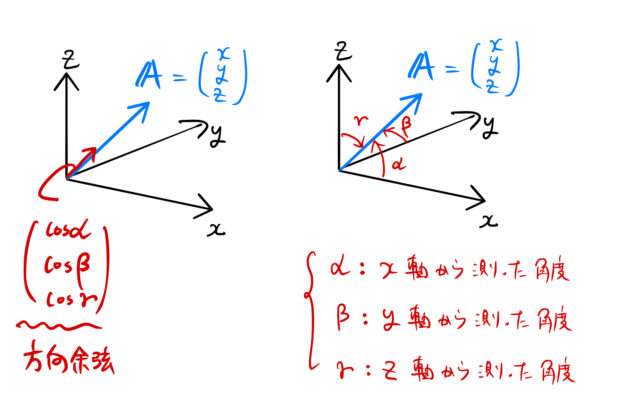



方向余弦 はじめての方向余弦 図でわかる ばたぱら




2直線のなす角を求める方法 方向ベクトル利用 おいしい数学




高校数学b ベクトルの内積の定義の成分表示となす角 垂直条件 受験の月




高校数学b ベクトルの垂直条件 映像授業のtry It トライイット



ベクトルの内積とは 意味 公式や求め方 計算問題 受験辞典



Math02 ベクトル Actionscript 3 0 For 3d




ゲーム数学 2つのベクトルのなす角度 ねこじゃらシティ




青チャート 空間ベクトルの内積 Clear




2直線のなす角を求める方法 方向ベクトル利用 おいしい数学
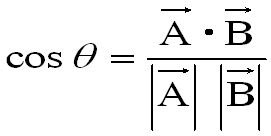



Angle2



06 幾何 17 ベクトルの内積や外積で3次元空間における面の向きを知りたい Flash Actionscript 3 0 Reference
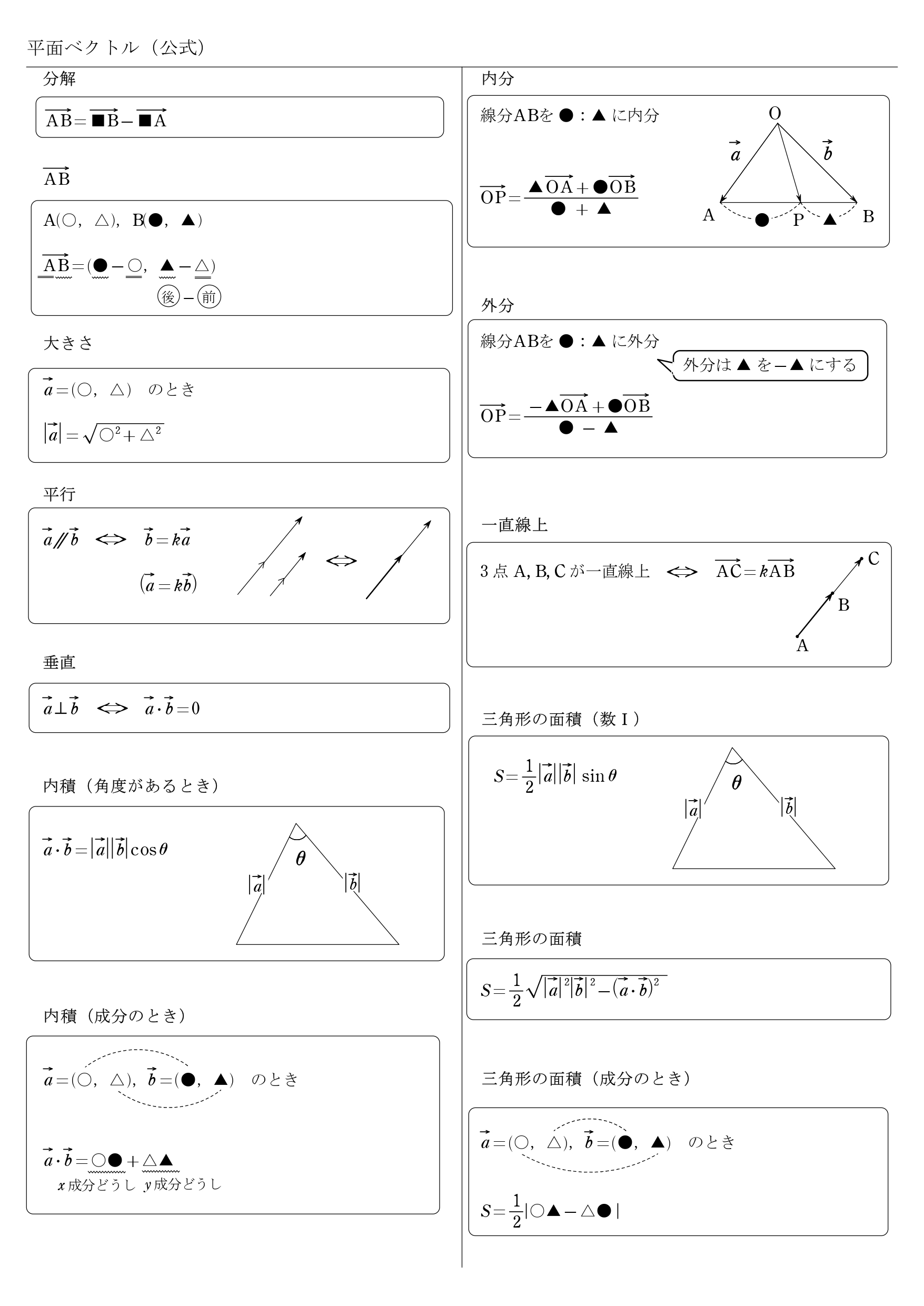



高校数学b 平面ベクトル 公式一覧 内分 外分 面積 学校よりわかりやすいサイト



二つのベクトルがつくる角度を求める Ng録



ベクトルの内積 スカラー積 と外積 ベクトル積 の成分表示



3dの覚え書き 基礎



1



Studydoctorベクトルのなす角と三角形の面積 数b Studydoctor



3




高校 数学b ベクトル14 なす角8 19分 Youtube



ベクトルの内積



3点からなる角度を求める 画像処理ソリューション




内積とは ベクトルの内積の意味 公式 求め方などをスッキリ解説 遊ぶ数学



内積とは 定義と求め方 公式を解説 ベクトルの掛け算を分かりやすく



ベクトル内積の意味をイメージで学ぶ 射影とは なす角とは ばたぱら




内積とは ベクトルの内積の意味 公式 求め方などをスッキリ解説 遊ぶ数学
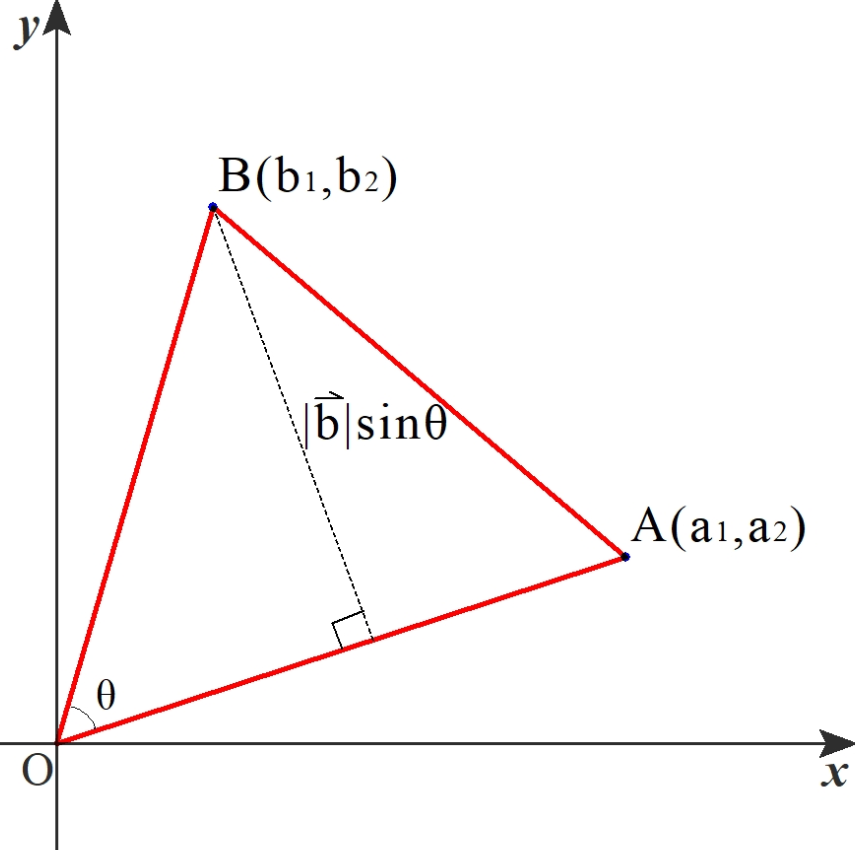



ベクトルを用いた三角形の面積公式3種類 数学の庭




高校数学b 空間の2直線 2平面 直線と平面のなす角 受験の月




数bの問題です 空間ベクトルの範囲です なぜ下線部のようになるかわかりません Clear



ベクトルによる三角形の面積の求め方 公式や証明 計算問題 受験辞典




高校数学b ベクトルのなす角の計算 練習編 映像授業のtry It トライイット



ベクトル演算 はじめに スカラー 大きさだけを持つ値 ベクトル 大きさと向きを持つ値 2点間のベクトル P1 50 25 P2 0 250 の指すベクトルp1p2 B1 A1 B2 より 150 225 極座標とデカルト座標によるベクトル表現 座標変換 三角関数の公式




方向余弦 はじめての方向余弦 図でわかる ばたぱら




標準 ベクトルの内積となす角 なかけんの数学ノート




Excel エクセルでベクトルの外積を計算する方法 外積の求め方




2つのベクトルの成す角



数学 内積ってなんぞ その2 角度とcg編 No More Retake



ベクトルの内積 スカラー積 と外積 ベクトル積 の成分表示




内積は求めれたんですが なす角8も余弦の求め方を教えてください 高校 教えて Goo




ベクトルの公式一覧 計算 内積 三角形の面積 共線条件 理系ラボ
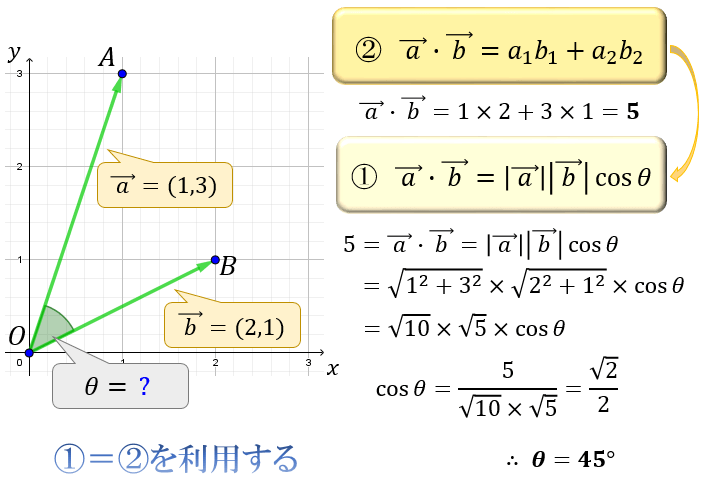



内積とは何なのか ベクトルの内積の2つの求め方とその活用法 アタリマエ




平面ベクトルの定義と公式 足し算 絶対値 内積 なす角の求め方 Irohabook




Java 2つのベクトルがなす角度を求める Shogonir Blog



2つのベクトルのなす角度を求める




高校数学b ベクトルの内積とax Byの最大最小 受験の月
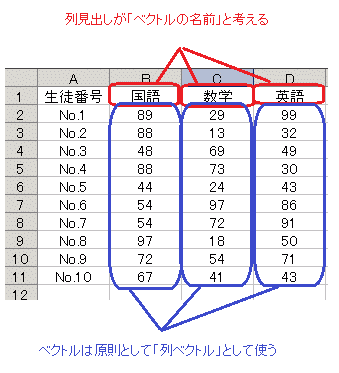



Excelを用いたベクトルの計算
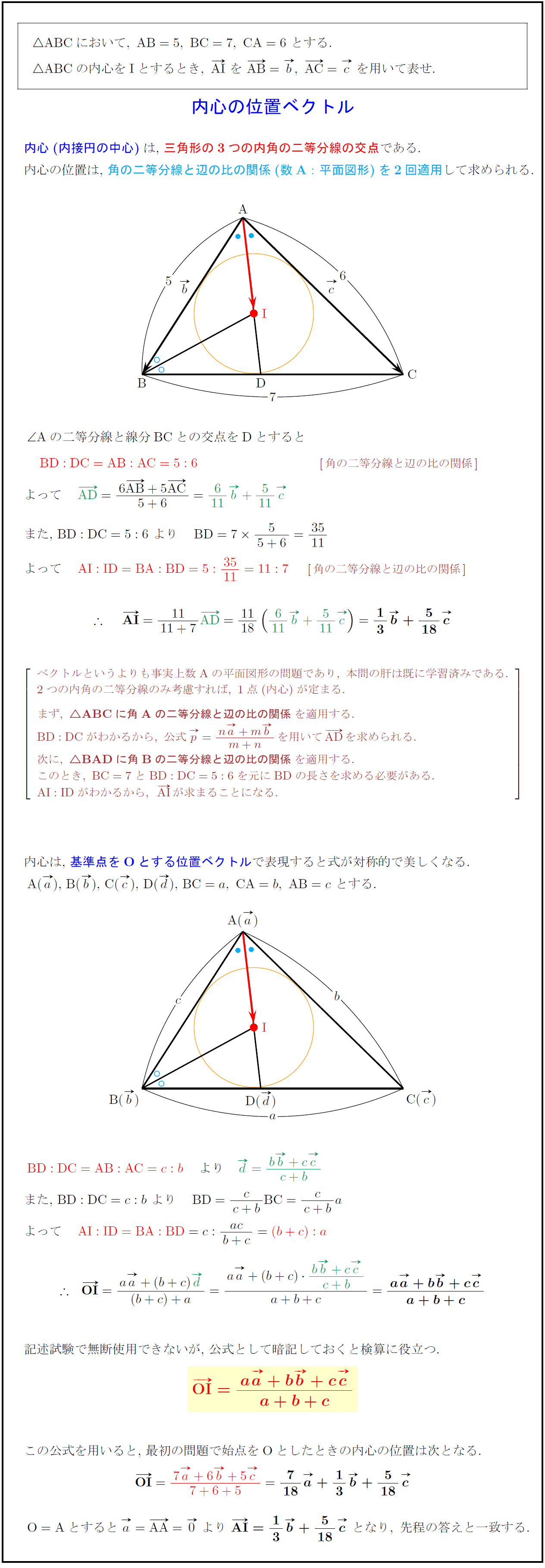



高校数学b 三角形の内心の位置ベクトル 受験の月
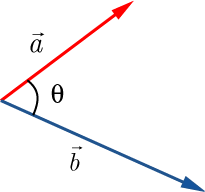



ベクトルのなす角



平面と平面のなす角度 Thoth Children
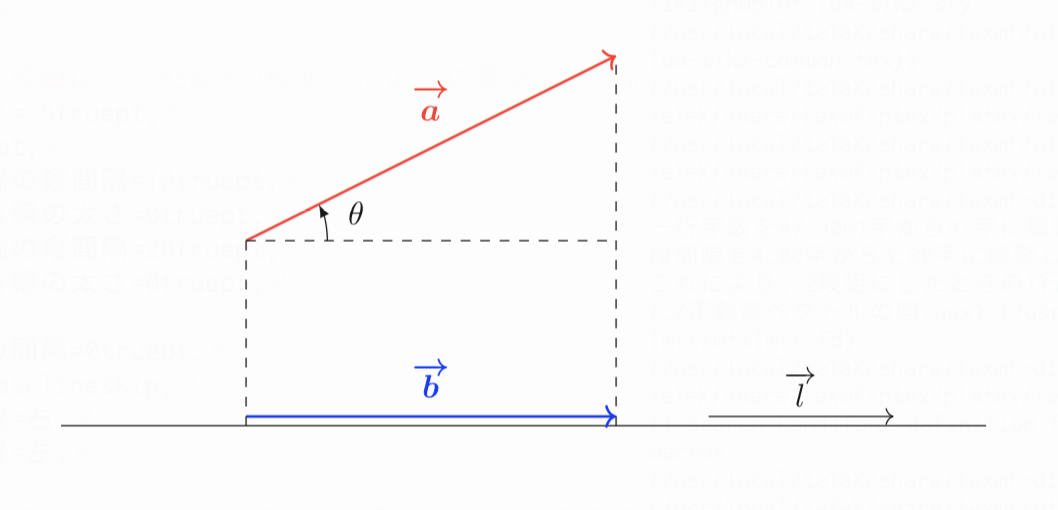



正射影ベクトルの公式は 平面や空間での入試問題を東大医学部生が解説 東大医学部生の相談室




内積の絡んだベクトルの問題 Youtube




高校数学 2直線のなす角とtan A B 例題編 映像授業のtry It トライイット
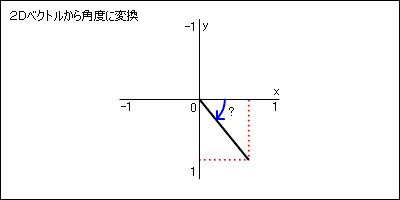



Flashゲーム講座 Asサンプル集 角度の計算について




ベクトルの内積の全てを超わかりやすくまとめた 意味 公式 成分計算 理系ラボ




高校数学b 空間ベクトルのなす角の計算 映像授業のtry It トライイット
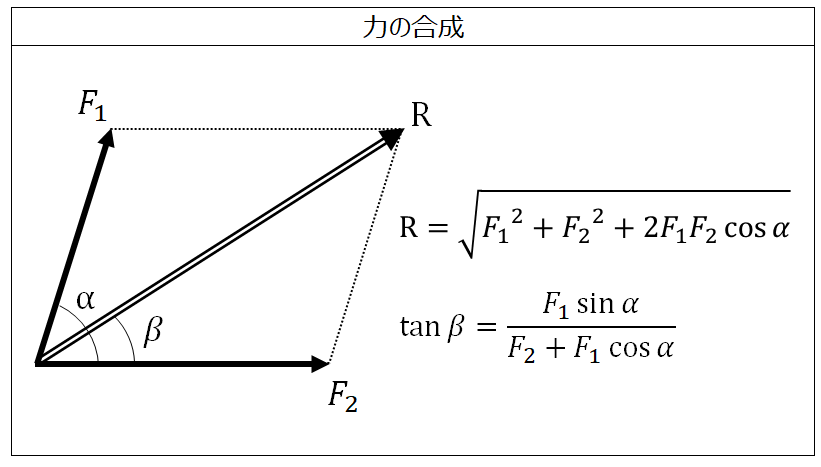



力の合成 合力の計算 任意の角度で交わる2力 製品設計知識
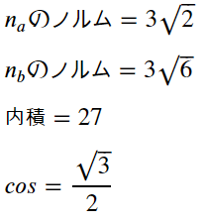



Pythonの内積 外積 ノルムに関する計算



0 件のコメント:
コメントを投稿