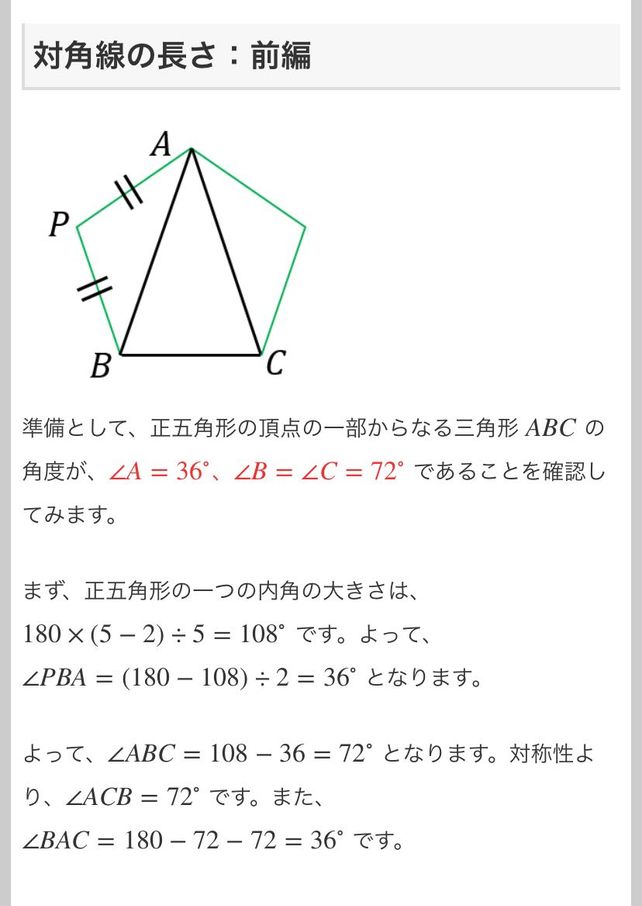
正五角形がイラスト付きでわかる! 全ての辺と角が等しい五角形。 概要 正多角形の一種であり、全ての辺の長さと角の大きさが同じな五角形である。 五角形の内角の和は540度なので、正五角形の内角は全て108度となる。 全ての対角線を結ぶと、五芒星(ペンタグラム)に、輪郭を取り出すと正五角形 の書き方 上の図の、辺cdと対角線acが描ければok ① cdを引く (2cm) ④ cfを引くと、ピタゴラスの定理より、 ⑥ 中心c,半径cgの円を描き、 ⑦ ciを底辺とする斜辺が2cmの 線分hfのf側に伸ばした延長線との 二等辺三角形を書く。長方形は円に内接する四角形なので,トレミーの定理が使えます。 長方形の辺の長さを a, b a,b a, b ,対角線の長さを c c c とおきます。トレミーの定理より「 上×下 + 左×右 =対角線のかけ算」なので a 2 b 2 = c 2 a^2b^2=c^2 a 2 b 2 = c 2 となります。これは

簡単公式 多角形の対角線の本数が5秒でわかる求め方 Qikeru 学びを楽しくわかりやすく
対角線とは 五角形
対角線とは 五角形-答948 五角形の面積の2等分 oa=oc=30,ob=od=x とすると、x の値の範囲は? ただし、内角が 180゚ の場合は五角形と見なさないものとし、 対角線adは 端点を除いて五角形oabcdの内部にあるも比 1 1 5 2 1\dfrac {1\sqrt 5} {2} 1 21 5 を 黄金比 (golden ratio)と呼び, 1 5 2 \dfrac {1\sqrt 5} {2} 21 5 を 黄金数 (golden number)と呼ぶ




正五角形の対角線からできた五角形は 正五角形ですか もし正五角形だったらどうやって Clear
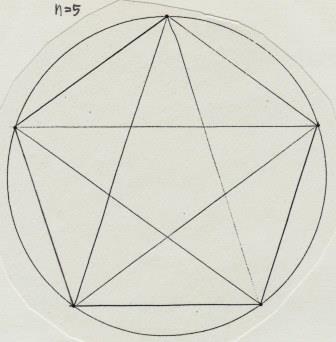
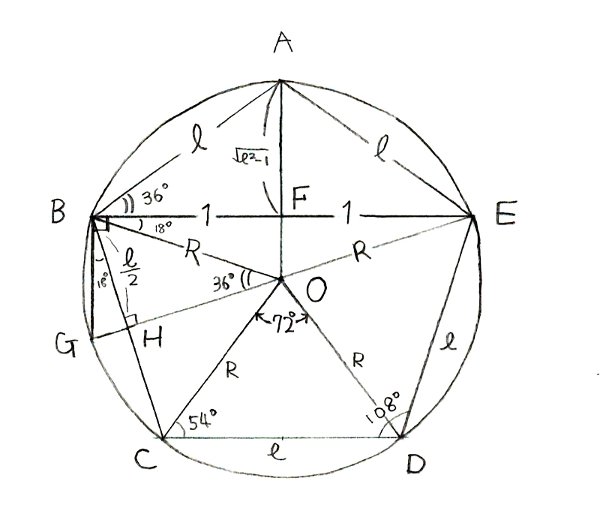
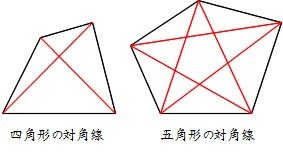
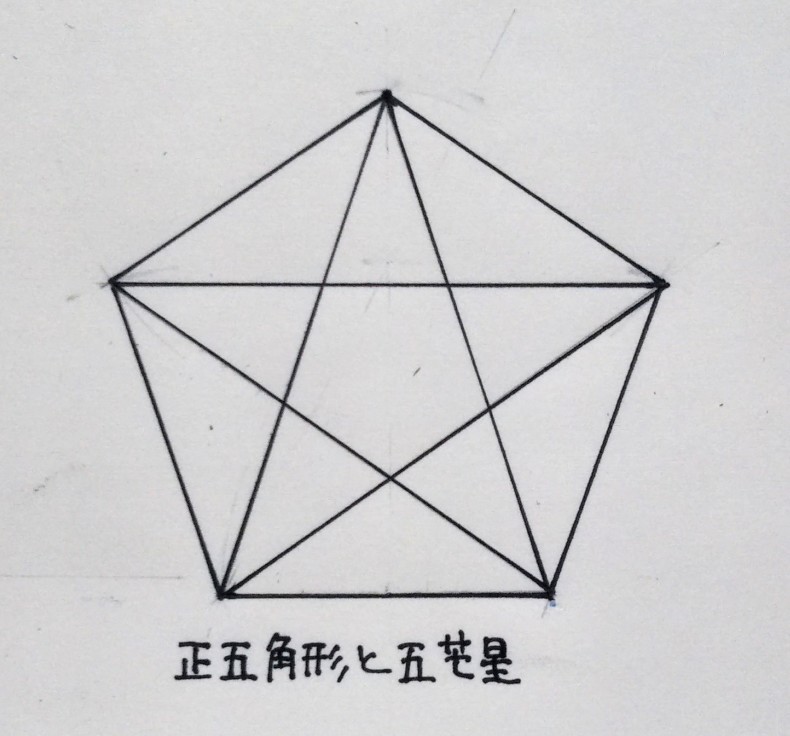
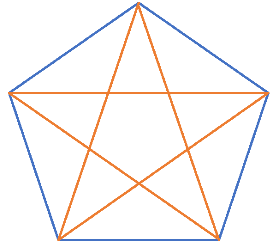
→正五角形の対角線の長さと高さ 方程式を解くことで求める 図形を使わずに $\cos 72^{\circ}=\sin 18^{\circ}$ の値を計算することもできます。Pを多角形の頂点に取り、 対角線で三角形に分ける。 内部の1点から出る線の数 三角形の数 角の和 内角の和=角の和-360° 四角形 五角形 六角形 七角形 八角形 n角形 (2) 頂点の数 辺上の1点から出る線の数 三角形の数 角の和 内角の和=角の和-180°ちなみに、対角線を引いた正五角形の中には、正五角形、平行四辺形そして等客台形(底辺でない2辺の長さの等しい台形)などの図形が隠れています。 たとえばのなどはペンタグラムとなっている。 切望! でも「宮城」ですか・・・(苦)><;!
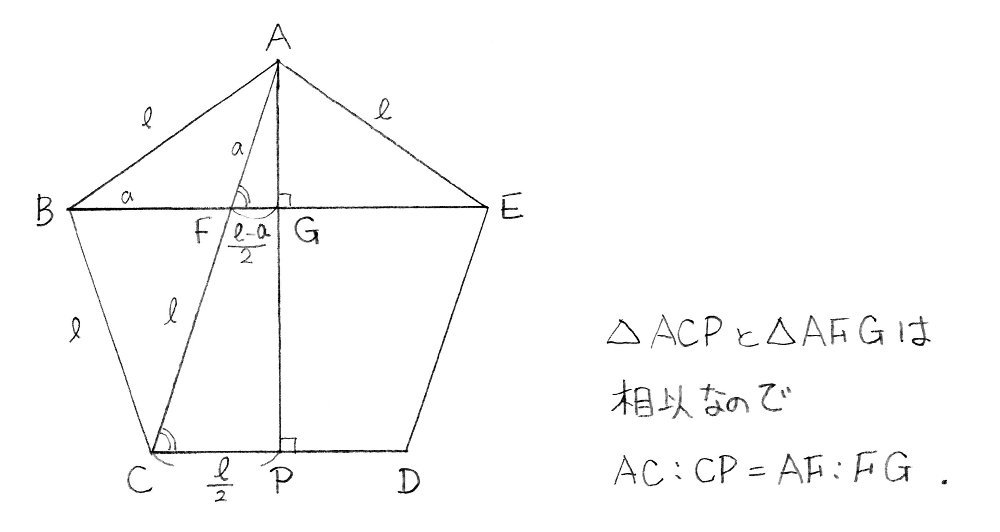
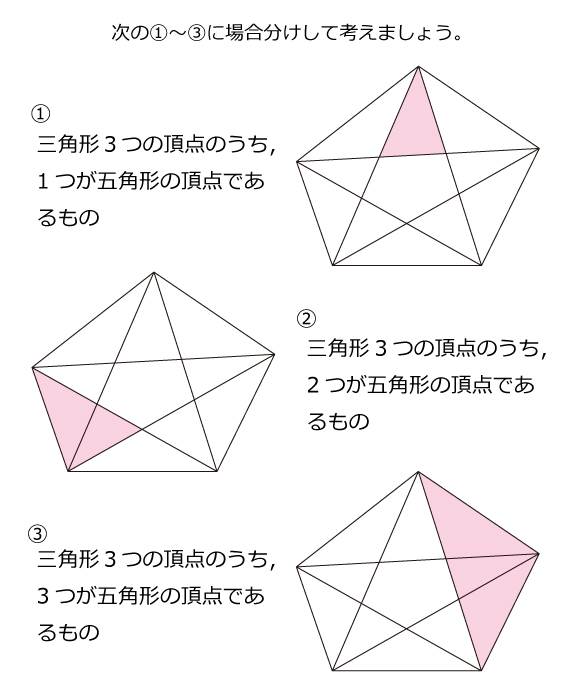
つまり, abfは直角三角形です。 ∠afoも90度となりますから, aof∽ acm したがって,aoac=ofcm 正五角形の1辺が1のとき対角線の長さは でしたから 正五角形の1辺が のとき対角線の長さは です。 これより, 比の性質から したがって, これから,問題4 凸25 角形の頂点を結んでできる五角形のうち,互いに辺や対角線を共有しないものをできるだけたく さん作れ. 解図5 のように各点を4 分の1 回転,正確には頂点6 個分ずらしてゆくと30 組の解を得られる. 6/9 正五角形の対角線でできる小さな正五角形の面積は? 一辺が長さ1の正五角形がある。 対角線を5本引くと、その内部に小さな正五角形ができます。 元の正五角形と内部にできる正五角形の面積の比を求めよ。 同じく正17角形の場合はどうなるか?
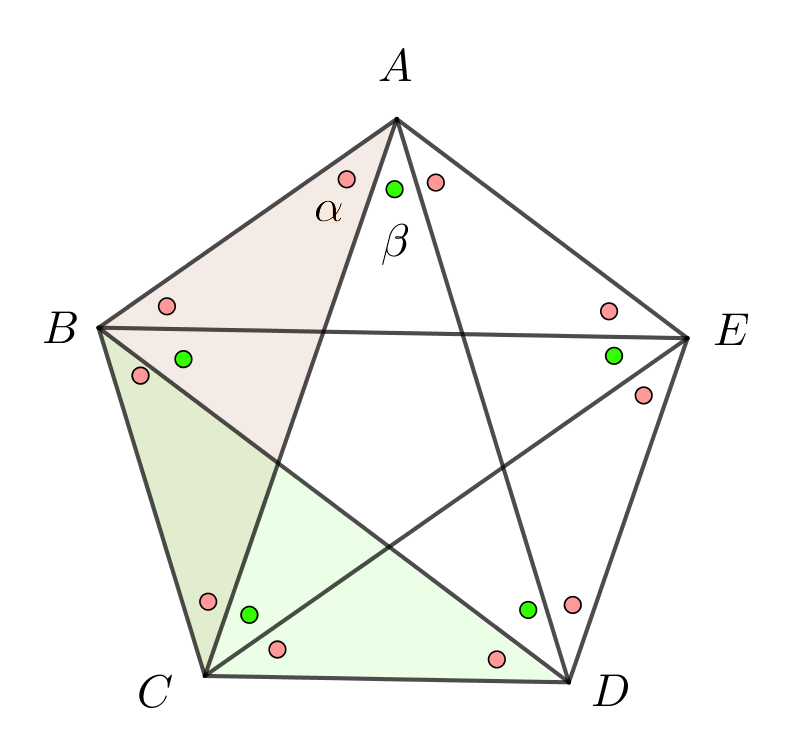
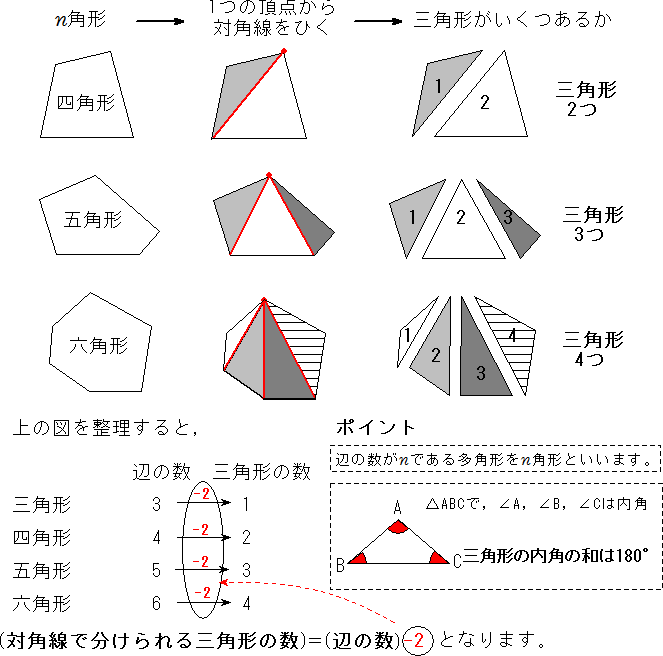
・五角形の角の和も対角線をひけば,計算でできることがわかった。 ・正がつく角は角度がすべて等しいことがわかった。 ・九角形も調べてみたい。 ・辺の数が多くなるにつれて角の大きさの和が180°ずつ多くなっていることがわかりました。 正五角形の辺と対角線が平行であることはどのように証明できますか? 正五角形をabcdeとしてbe平行cdを示すとしたら、 四角形bcdeにおいて∠b=∠e ∠bde=∠cdeより対角の和が180°であることなど、いろいろ示すことはできるのですが結局どうつなげばいいかわかりません。 五角形の対角線の本数を求めてみよう。 公式のnに「5」を代入すればいいから、 n (n3)÷2 = 5× (53)÷2




相似19 正五角形と黄金比 Youtube




正五角形の対角線の長さと作図方法 高校数学の美しい物語
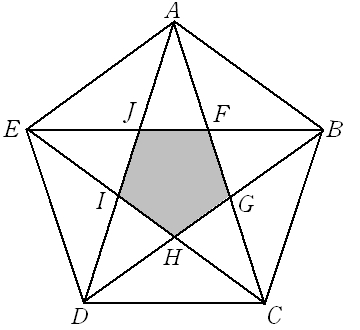
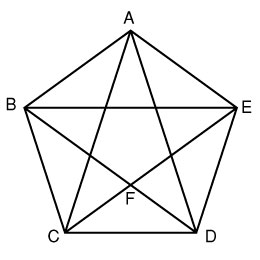
概要 編集 直交対角線四角形は、向かい合う辺の長さの2乗の合計はもう一方の向かい合う辺の長さの2乗の合計と等しくなる 。 = これは、ピタゴラスの定理に基づいている。 これはまた、余弦定理、空間ベクトル、背理法、複素数の使用など、さまざまな方法で証明できる 。正五角形の対角線と外接円 △ACD,△CDL は頂角 36°の二等辺三角形,△LAC は頂角 108°の二等辺三角形であり AL = CL = CD = 1 である.対角線の長さを AC = AD = x とすると,△ACD と △CDL は作図で重心を見つける方法の質問だと解釈し、説明します。 正五角形の対角線は下図の青線のようになり、これだけでは重心が見つかりません。 下図の対角線 と の交点を 、同様に、, , , を定めていきます。 すると、 と の交点が正五角形の重心となり




正五角形の対角線からできた五角形は 正五角形ですか もし正五角形だったらどうやって Clear



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
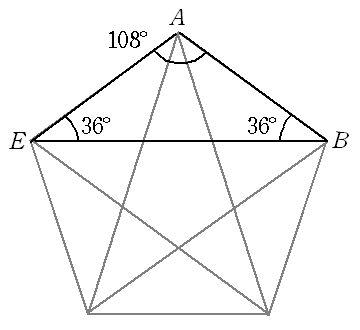
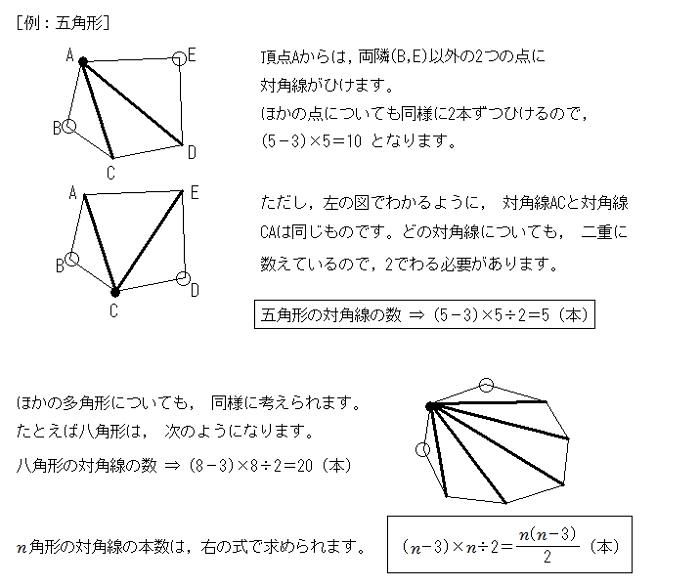
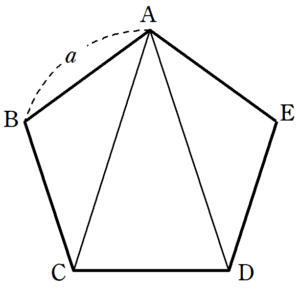
正五角形の頂角は 108 度です。 それは次の式から求めることができます。 対角線BE と 対角線AD の交点をFとします。 FEAは二等辺三角形です。 FE = FA です。 BFAは二等辺三角形です。正五角形の∠aの二等分線と辺cdとの交点をmとする。 a 対角線ceとamの交点をpとするとき, 対角線dbもamと点pで交点を持つことを 説明しなさい。 (問3の結果を使いなさい) 答え正五角形はamについて線対称であるから, 点cはamについてdに重なり,点bはeに重なる対角線の本数 1 ステップ1 計算で求める 1 図1のように、五角形には5本の対角線があります。 この対角線の本 数を、計算で求めようと思います。 ⑴ 図2のように、頂点Aからは( )本の対角線が引けま



正五角形を描く ウソの国ー詩と宗教 戸田聡 St5402jp
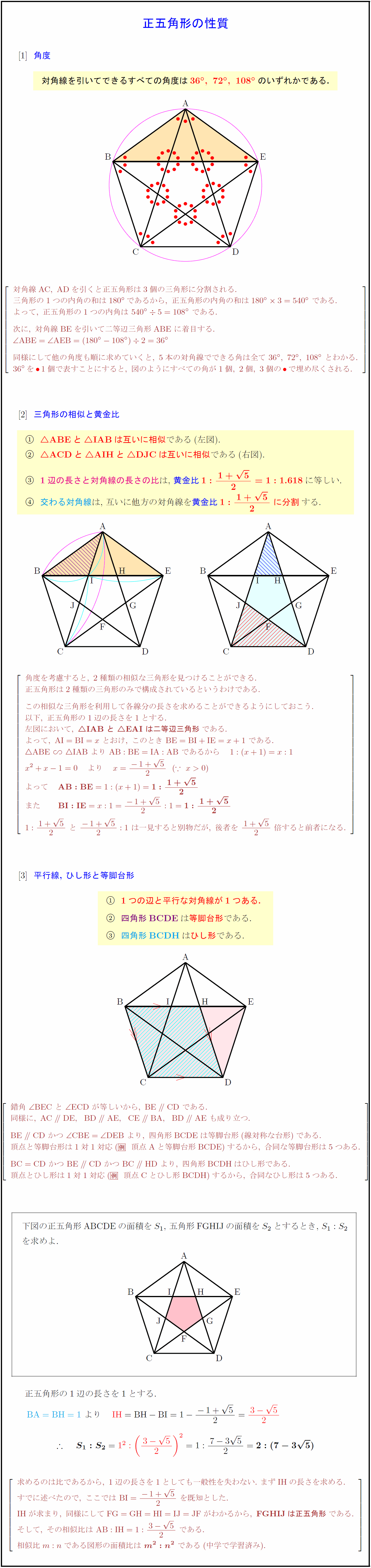



高校数学a 正五角形の性質 三角形の相似 黄金比 等脚台形 ひし形 受験の月
数学・算数 数学の問題です 1辺の長さが1の正五角形abcdeにおいて、対角線ac,beの交点をfとし、∠abe=θとおく。 abeと fabは相似である。 線分bfと線分beの長さを求めよ。こ 質 実は {1辺の長さ1の正5角形の辺と対角線の一部の図}であることを認識しておけば忘れない この背景があるため,\ sin18°,\ cos36°を求める場合に限らず様々な場面で現れる図である ちなみに,\ { (1辺) (対角線)=BCAB=1 {15} {2}}\ がいわゆる {黄金比}である対角線の長さが互いに全て等しい正多角形は、正五角形と 正四角形 (正方形)のみである。 n 角形の対角線の本数を m 本としたとき n = m が成り立つのは n = 5、すなわち五角形だけである。



1
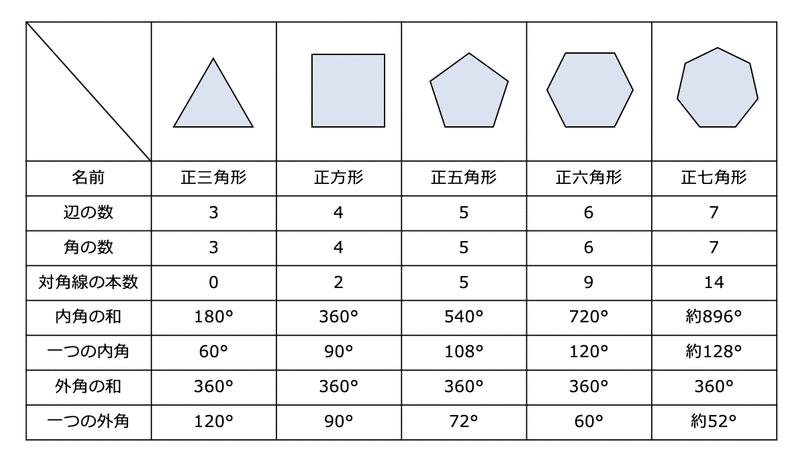



実践例 プログラミングで正多角形を学ぶ 山崎智仁 Tomohito Yamazaki Note
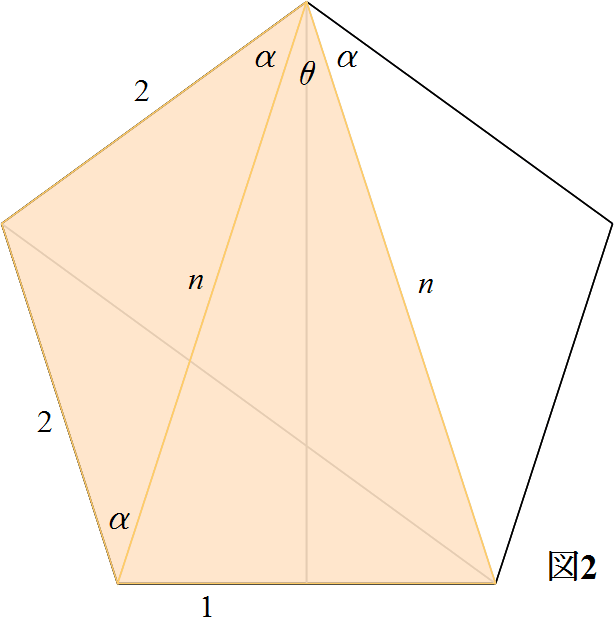
五角形は図のように対角線を引くと, 三角形が3つできる。 三角形の内角の和は180°だから 答え 540° 前の時間で四角形の内角の和を求めた時のことを思い出して,これらの図形の 内角の和を求めてみましょう。 ② ① ③ 自分の考え形が分かるように図に も正五角形の対角線の長さ / 一辺の長さ=黄金比を示す172の証明 / 若原龍彦 〔本〕 在庫状況は商品詳細のリンク先を確認下さい お気に入り 2,090 円 + 送料495円 (全国一律)折り紙で正五角形をつくる 正五角形の 辺の長さが のとき対角線の長さは だから,対角線の長さが のとき 辺の長さは である。折り紙の 辺の長さを とする。
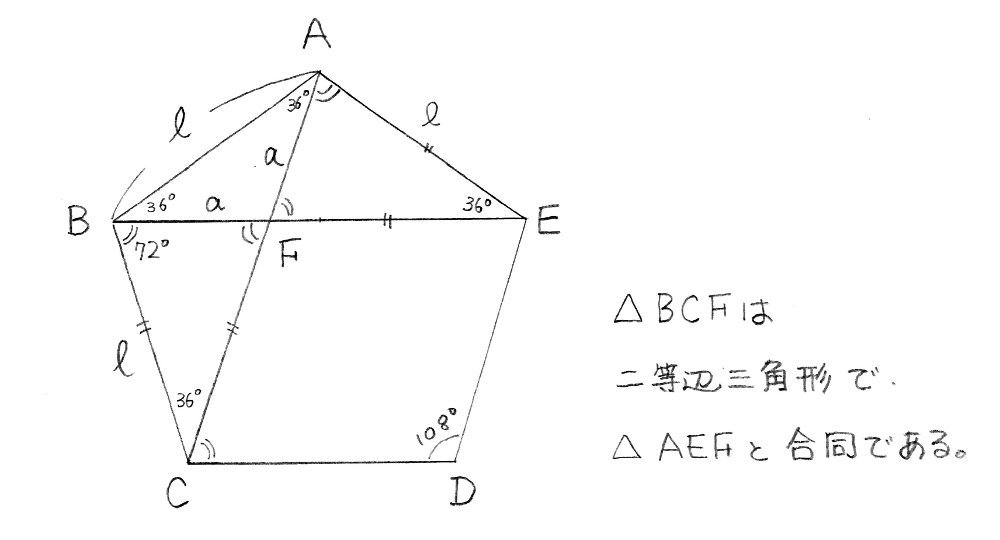



五角形5 辺と対角線の比 Wandering In The Woods




簡単公式 多角形の対角線の本数が5秒でわかる求め方 Qikeru 学びを楽しくわかりやすく
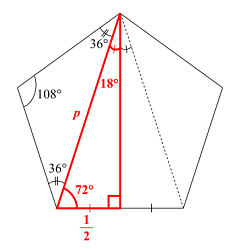
予習シリーズ小5上第1回と対応します。必修レベル内角の和・外角の和 五角形の内角の和は、何度か。 正五角形の1つの内角の大きさは、何度か。 内角で求めるか、外角で求めるかの2パターンある。内角で求める解き方1つの角度を聞い 正五角形の一辺の長さと対角線の比が黄金比であることは有名ですが、導出の方法を考えてみました。 図1正五角形の辺と対角線で作る三角形 図1 のように、正五角形の1つの辺と2つの対角線でできる二等辺三角形と、それを半分にした直角三角形を考える正五角形関連 編集 五角形の対角線を繋いだ星形を五芒星(ペンタグラム)という。 たとえば長崎市の市章などはペンタグラムとなっている。;



黄金比の直角三角形の垂線と正五角形の外接円の半径 教材作家
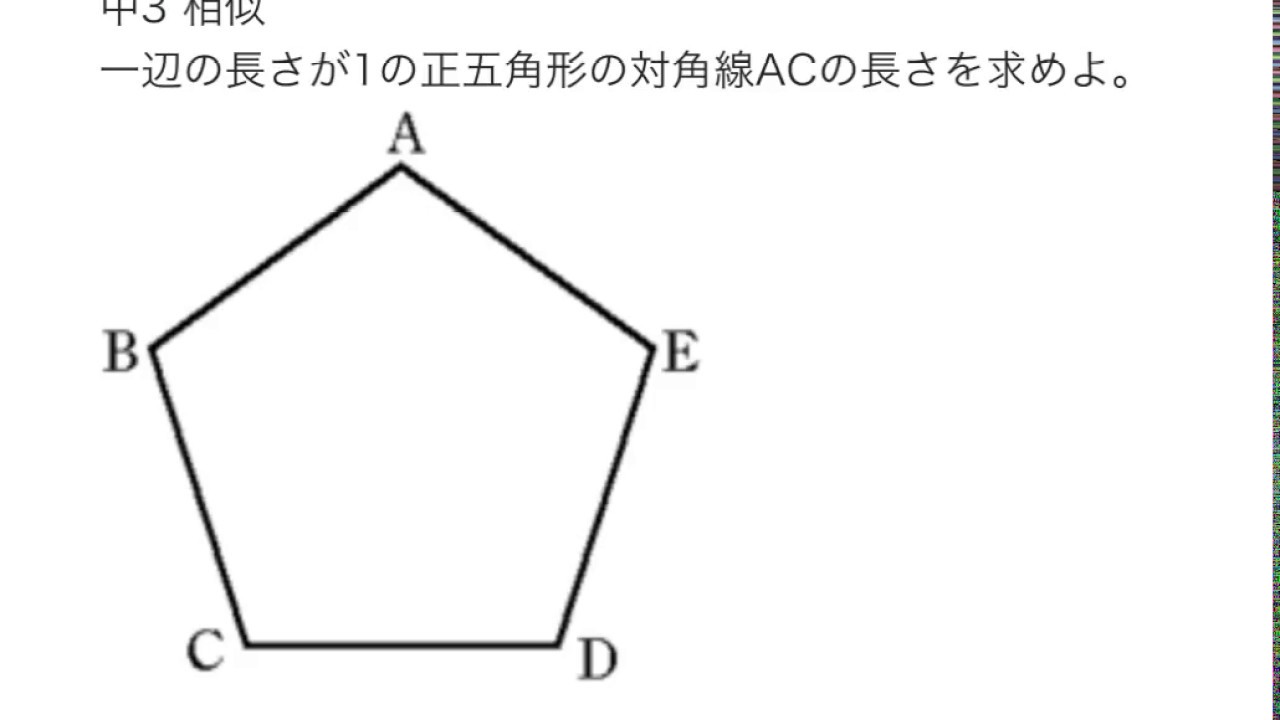



中3相似 正五角形の対角線の長さを求める問題 Youtube
よって,正五角形の2 本の対角線は,それらの交 点において黄金比に内分されることが分かる. 図10 のように正五角形や五芒星は入れ子状に無 数に描くことができ,部分と全体が相似となるフラ クタル構造を有していることが分かる.




正五角形に付随する角度と黄金比の関係 萌えとかプログラミングとか



My Math Note




正五角形の対角線の長さ 一辺の長さ 黄金比を示す172の証明 若原 龍彦 本 通販 Amazon



一辺の長さがの正五角形の対角線の長さはいくつか 解説お願いします 正五角 Yahoo 知恵袋




桜の美しさの背後には 数学的な秘密があるかも 春の花から見えてくる正五角形 ナンスカ
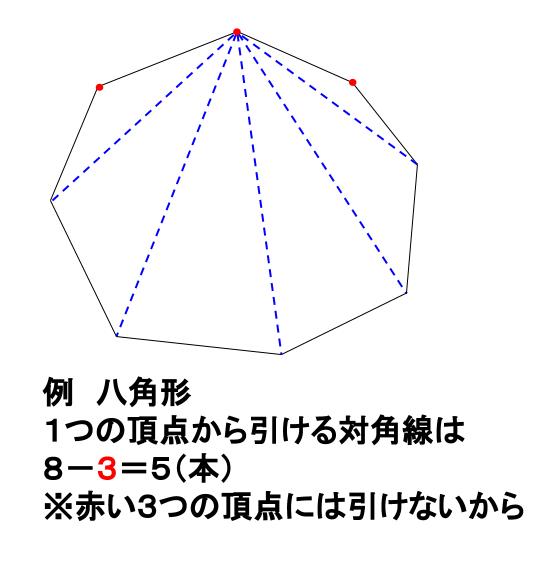



中学数学 多角形の対角線の本数 中学数学の無料オンライン学習サイトchu Su



五角形の対角線の数に公式があった 数学のヒント



正多角形の対角線 あなたと夜と数学と
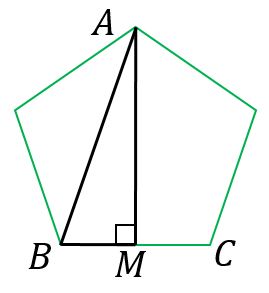



正五角形の対角線の長さと高さ 具体例で学ぶ数学



一辺が2センチの正五角形の対角線の長さを求めるのをお願いします Yahoo 知恵袋



Q Tbn And9gcsk3iooe0glw6r2emrvfhyuy5donjyjtkxf7fg Abxgmzsqhp Usqp Cau




解説お願いします 人 Clear




正多角形の対角線



Uvtf344 Xwmusm
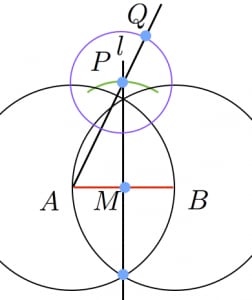



正五角形の対角線の長さと作図方法 高校数学の美しい物語




正五角形の対角線の長さ 一辺の長さ 黄金比を示す172の証明の通販 若原 龍彦 紙の本 Honto本の通販ストア



五角形に思いを馳せる 今と私が大学生だった時代を比べると 一番違うのが電話を含めたit Pc 関係の環境であることは間違いない 次がタバコを取り巻く環境だろうと個人的には思っています 昭和から平成の時代となり アナログから




Formula60 正五角形の対角線 難関高校合格のための中学数学公式一覧 10秒で解けますか




対角線とは 多角形の対角線の本数の2通りの求め方 算数パラダイス




Lihat Cara Penyelesaian Di Qanda




正多角形の対角線の長さの種類 香料ゐっすゐの夢



図形 正五角形の分解 父ちゃんが教えたるっ




答1485 五角形の対角線の長さ ヤドカリの 気ままな数学
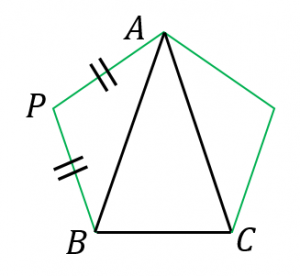



正五角形の対角線の長さと高さ 具体例で学ぶ数学




簡単公式 多角形の対角線の本数が5秒でわかる求め方 Qikeru 学びを楽しくわかりやすく



組合せの対角線の問題で正五角形の求め方を教えてください Yahoo 知恵袋
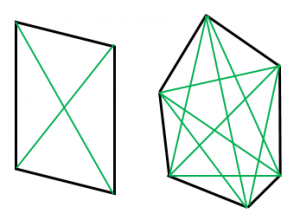



多角形の対角線の本数を求める公式 具体例で学ぶ数学



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典




黄金三角形による18 シリーズの三角比 おいしい数学



茗渓予備校 科目別データベース



多角形の内角の和 勉強ナビゲーター



対角線 何本かな Gnolink 個別指導 グノリンク 知の力を活かせる人に




正五角形の対角線の長さ 高校入試数学 大学入試数学 Youtube



これは誤解 これが正解




17 四苦八苦する黄金比と白銀比 空 殻 核 くうからかく



算数にチャレンジ




対角線 Wikipedia



炉辺夜話 数学編 第2夜 正五角形を描こう



対角線 何本かな Gnolink 個別指導 グノリンク 知の力を活かせる人に



五角形3 辺と対角線の比 Wandering In The Woods



三角形と四角形 多角形の内角の和 中学数学 定期テスト対策サイト




ヨドバシ Com 正五角形の対角線の長さ 一辺の長さ 黄金比を示す172の証明 単行本 通販 全品無料配達



3 多角形の重心



正五角形の辺と対角線の比 数学自由研究



図形 正五角形の分解 父ちゃんが教えたるっ




正五角形の対角線でできる小さな正五角形の面積は Okwave




正五角形とその対角線によって囲まれてできる正五角形との面積の比 身勝手な主張




十五角形 Wikipedia
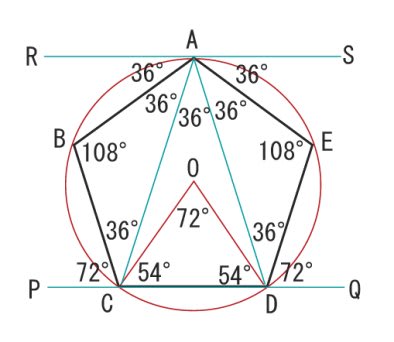



正五角形というだけで 分かる角度は 名寄 算数数学教室より
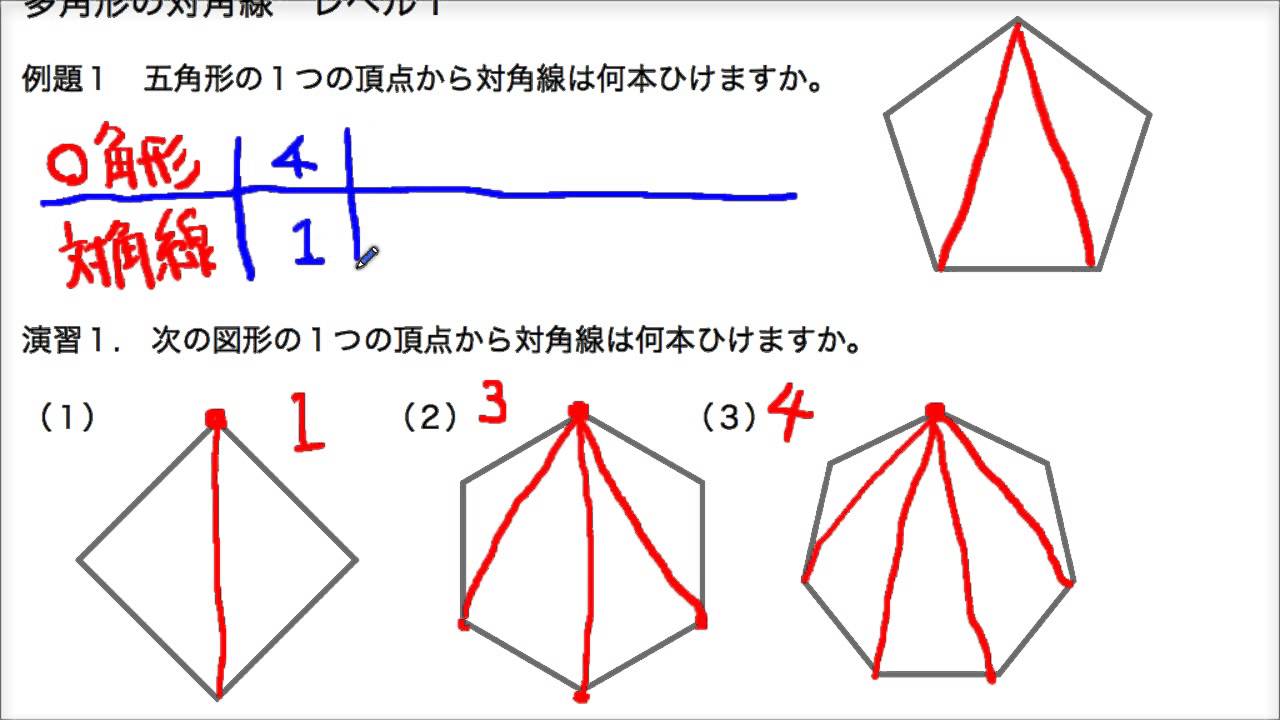



多角形の対角線 多角形と角 レベル1 中学受験 算数 Youtube



3




高校数学b ベクトルと正五角形 Cos108 の値 受験の月



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典



正五角形の重心はどのようにして見つけますか Quora




簡単公式 多角形の対角線の本数が5秒でわかる求め方 Qikeru 学びを楽しくわかりやすく
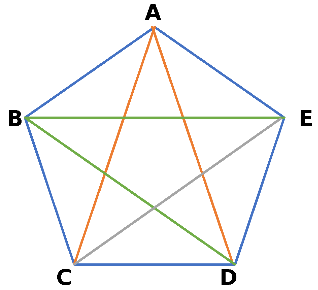



対角線 何本かな Gnolink 個別指導 グノリンク 知の力を活かせる人に
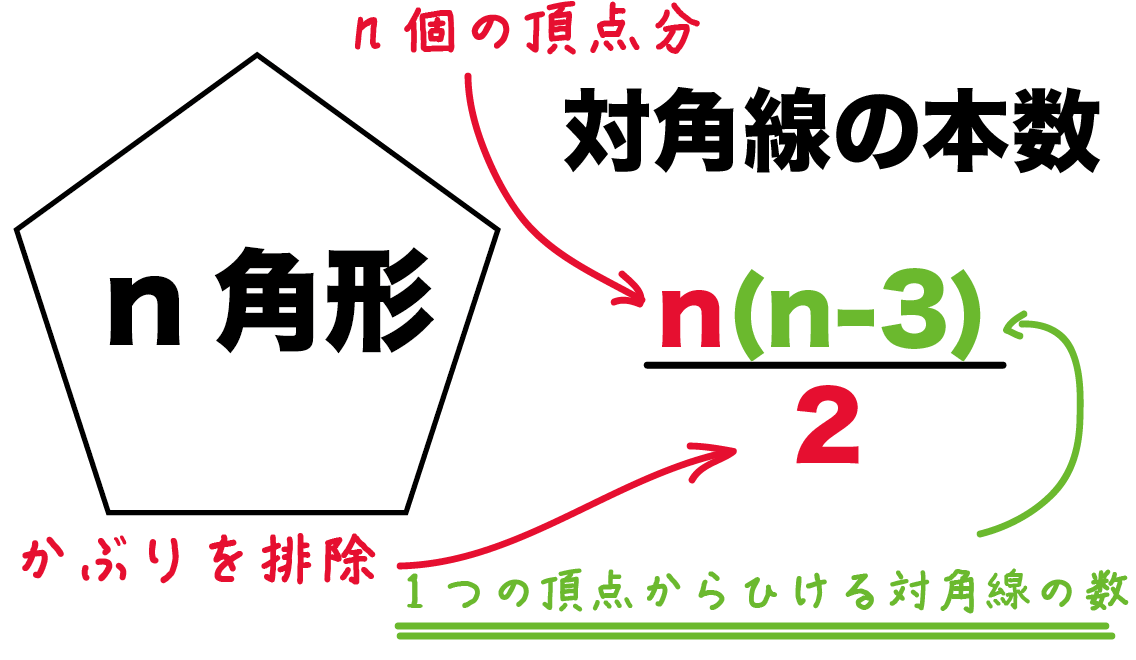



簡単公式 多角形の対角線の本数が5秒でわかる求め方 Qikeru 学びを楽しくわかりやすく



7 O5 A B C D E Abcde A A Descubre Como Resolverlo En Qanda



茗渓予備校 科目別データベース



五角形5 辺と対角線の比 Wandering In The Woods



茗渓予備校 科目別データベース



Math 対角線の数 働きアリ
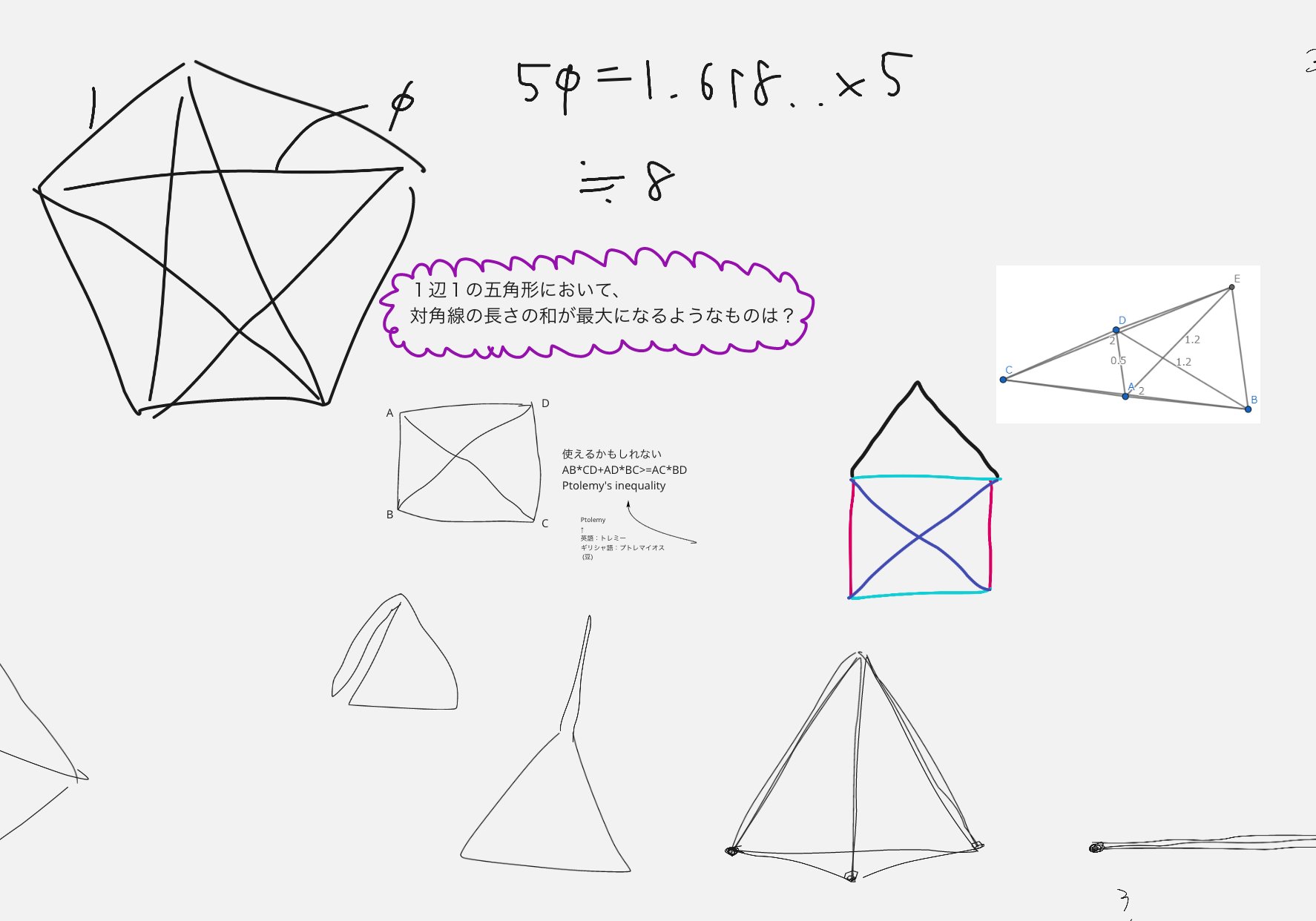



Uzivatel 鯵坂もっちょ Na Twitteru 1辺1の五角形の対角線の長さの和を最大にする問題けっこう面白い 凸関数に関する不等式 イェンゼンの不等式 で瞬殺されていたが拡張の方向性がいろいろあってもう少しコスれそう 数学デー オンライン数学デー




正五角形に付随する角度と黄金比の関係 萌えとかプログラミングとか



第65問の解答



ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス




z会 Asteria No Twitter う 数学 正五角形を題材とした 面積が等しい 図形2 材料 正五角形 1個 対角線 5本 正方形 大1個 中3個 小1個 作り方 1 正五角形に対角線を添える 2 赤色と青色 分量外 で正方形に下味をつける 3 画像のように正方形を



数学切り抜き帳



黄金比と五角形 獺祭亭日乗




正五角形の対角線の長さ 一辺の長さ 黄金比を示す172の証明の通販 若原 龍彦 紙の本 Honto本の通販ストア




簡単公式 多角形の対角線の本数が5秒でわかる求め方 Qikeru 学びを楽しくわかりやすく



三角形と四角形 対角線を求める問題 中学数学 定期テスト対策サイト



図形ドリル 第140問 正五角形の対角線 算数星人のweb問題集 中学受験算数の問題に挑戦




正五角形の長さや面積の導出 数学の偏差値を上げて合格を目指す




1 12 2 1 Descubre Como Resolverlo En Qanda




58ばんが 答えを見てもよく分からないです 教えてください Clear



対角線 何本かな Gnolink 個別指導 グノリンク 知の力を活かせる人に




正五角形とその対角線によって囲まれてできる正五角形との面積の比 身勝手な主張



正五角形の対角線の長さ 一辺の長さ 黄金比を示す172の証明 通販 Lineポイント最大0 5 Get Lineショッピング




簡単公式 多角形の対角線の本数が5秒でわかる求め方 Qikeru 学びを楽しくわかりやすく



正多角形の面積の公式 Fukusukeの数学めも




対角線とは 多角形の対角線の本数の2通りの求め方 算数パラダイス




My Math Note



1




相似19 正五角形と黄金比 Youtube



早急でお願いします 正五角形の辺cdの長さと対角線acの長さの Yahoo 知恵袋



ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス
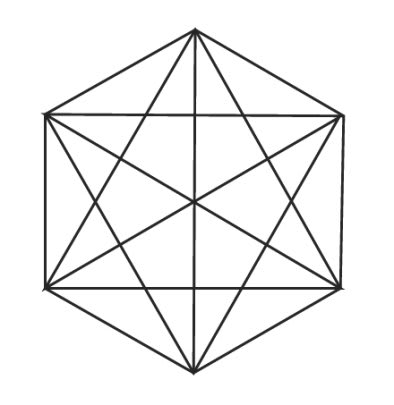



対角線の数って どうやって計算するんだ 名寄 算数数学教室より
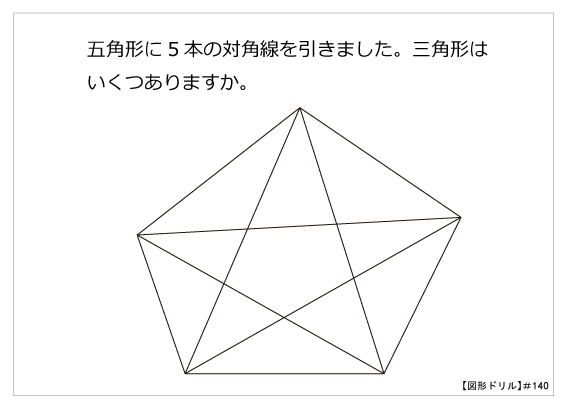



図形ドリル 第140問 正五角形の対角線 算数星人のweb問題集 中学受験算数の問題に挑戦
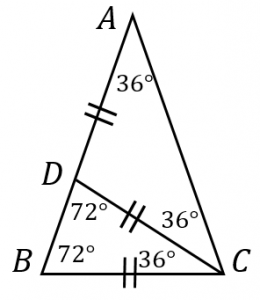



正五角形の対角線の長さと高さ 具体例で学ぶ数学



正五角形に対角線を引いて中に星を書きましたゼンブでいくつの三角形がある Yahoo 知恵袋




正五角形の長さや面積の導出 数学の偏差値を上げて合格を目指す



0 件のコメント:
コメントを投稿